Tutorial Statistik: 2016

Analisis Regresi Linier Sederhana dan Berganda

Analisis Regresi digunakan untuk mengetahui apakah suatu fenomena menyebabkan suatu fenomena yang lain atau dikenal dengan hubungan sebab dan akibat. Dalam penelitian eksplanatori diperlukan analisis regresi untuk mengetahui penyebab dalam suatu fenomena lalu dirumuskan dalam sebuah persamaan yang dinamakan Persamaan Struktural.

Suatu fenomena dijelaskan dalam sebuah variabel yang dinamakan X serta bagaimana pengaruhnya terhadap fenomena yang lain dalam sebuah variabel Y.
X merupakan variabel bebas (Independen) yang artinya tidak dipengaruhi oleh apapun sedangan Y adalah variabel terikat (Dependent) yang keberadaanya dipengaruhi oleh variabel lain yakni X.

Umumnya membutuhkan waktu yang lama dalam melakukan analisis regresi ini. Dengan adanya SPSS analisis regresi dapat dilakukan dengan lebih mudah.

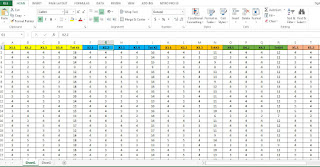
Pertama kita akan mengetahui bagaimana lihat pengaruh Variabel X terhadap Y dalam dengan analisis regresi. Langkah pertama Input Data seperti di bawah ini menggunakan Excel seperti berikut:

Data diatas merupakan Input yang akan digunakan dalam regresi. Data dapat diunduh di penjelasan sebelumnya tentang Input Data. Setelah dibuat data tersebut maka yang kita butuhkan adalah Nilai Total Skor masing-masing Item Pertanyaan atau Rata-rata Total Skor Item pertanyaan yang kita notasikan sebagai Variabel X1 sampai X5 dan Y.

Masing-masing nilai rata-rata atau total skor kita masukkan dalam SPSS dengan metode Stepwise yakni satu persatu dengan menulis variabel X1 sampai Y lalu di copy paste dalam kolom SPSS seperti dibawah ini:

Data diatas menggunakan nilai rata-rata walaupun sebenarnya bisa mengambil dari nilai total skor.

Langkah pertama dalam melakukan analisis Regresi Sederhana adalah Klik Analyzed---> Regression ---> Linear seperti pada gambar dibawah ini

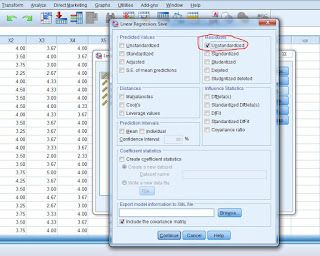
Setelah itu akan muncul kotak dialog seperti pada gambar di bawah ini:

Karena ini adalah percobaan untuk Regresi Sederhana maka masukkan satu variabel saja yakni X1 pada kolom Independent dan Variabel Y pada kolom Dependent lalu Klik Ok maka hasilnya adalah sebagai berikut:

Hasilnya adalah seperti itu. Tabel tersebut akan dijelaskan dalam tahap yang sebenarnya di Analisis Regresi Berganda.

Pembahasan difokuskan kepada analisis regresi berganda karena analisis regresi linier sederhana sudah jarang dilakukan dalam penelitian. Oleh karena itu kita langsung ke Inti ketika variabel bebas lebih dari satu.

Dalam melakukan Analisis Regresi Berganda tidak mudah dilakukan karena harus memenuhi Asumsi yang dibutuhkan agar sebuah model persamaan dapat dikatakan baik. Asumsi tersebut adalah Asumsi Klasik yang akan dijelaskan dalam Sub Bab ini Uji Asumsi Klasik

Setelah persamaan memenuhi Asumsi Klasik tersebut maka dapat dilakukan Analisis Regresi Beganda.

Langkah pertama adalah seperti yang dijelaskan tadi Analyze ---> Regression ----> Linear maka akan muncul kotak dialog dibawah ini:

Pada kotak dialog diatas masukkan variabel X1, X2, X3, X4 dan X5 pada kolom Independent dan Y pada kolom Dependent lalu Klik OK. Hasilnya seperti di bawah ini:

Hasil analisis yang dibutuhkan dalam analisis Regresi antara lain sebagai berikut:

1. Analisis Koefisien Determinasi (R- Square) / Uji Goodness of Fit
Analisis Koefisien Determinasi adalah melihat berapa persen kontribuasi variabel X1 sampai X5 terhadap Y. Semakin banyak variabel maka persentasenya akan semakin besar. Persentase ini dapat dilihat dari nilai R Square. Nilai Rsquare hasil regresi diatas adalah 0,506 maka bila dijadikan persen makan menjadi 50,6%. Berdasarkan hasil tersebut diketahui bahwa X1 sampai X5 dapat menjelaskan Y sebesar 50,6% atau Kontribusi X1 sampai X5 adalah 50,6%. Sisanya 49,4% dijelaskan oleh variabel lain.

2. Analisis Pengaruh Secara Simultan (Uji F)
Analisis pengaruh variabel X1 sampai X5 terhadap Y dilihat secara keseluruhan atau Simultan melalui Uji F. Uji F dapat dilihat pada tabel Anova. Berdasarkan hasil diatas maka pengaruh Variabel X1 sampai X5 secara keseluruahn dapat dikatakan memiliki pengaruh yang signifikan karena memiliki nilai Signifikansi dibawah 0,05 yakni 0,00<0,05.

3. Analisis Pengaruh secara Parsial (Uji t)
Analisis pengaruh secara parsial adalah melihat pengaruh X1 sampai X5 terhadap Y secara terpisah atau satu persatu. Dilihat pada hasil variabel yang dikatakan memiliki pengaruh bila dalam Uji t signifikansi pada tabel Coeficients dibawah 0,05. Berasarkan hasil tersebut hanya satu variabel yang tidak berpengaruh signifikan yakni X1 karena nilai signifikannsinya diatas 0,05 (0601>0,05). Sedangkan Variabel yang lain memiliki pengaruh yang signifikan karena nilai signifikansi dibawah 0,05.

4. Analisis Persamaan Regresi
Berdasarkan hasil uji t dapat dibuat sebuah persamaan dengan melihat kolom Beta Unstandardized di tabel Coeficients. Angka pada kolom tersebut disebaut dengan Koefisien Beta untuk variabel X2 sampai X5 (X1 tidak dimasukkan karena tidak memiliki pengaruh yang signifikan) sedangkan yang diatas adalah Konstanta dinotasikan dengan huruf alpha atau a. sebuah persamaan yang dapat dirumuskan adalah sebagai berikut:

Y= a+ BX2 + BX3 + BX4 + BX5

Y= -0,213 +0,185X2 + 0,273X3 + 0,202X4 + 0,250X5

Berdasarkan persamaan tersebut dapat dikatakan bahwa peningkatan X2 akan menghasilkan peningkatan Y sebesar 0,185. Begitu juga seterusnya untuk X3 sampai X5. Namun jika lihat secara keseluruhan yakni X2 sampai X5 maka peningkatan Y perlu djumlahkan dengan Konstanta.

Demikian latihan analisis Regresi dan Regresi Berganda semoga bermanfaat.

Uji Asumsi Klasik

Dalam melakukan analisis regresi berganda akan terdapat banyak faktor yang harus dipenuhi terlebih dahulu mengingat bahwa X terhadap Y lebih sederhana ketika menambahkan X1, X2. X3.X4 hingga X5 terhadap Y. Asumsi inilah yang disebut dengan Asumsi klasik dan harus diselesaikan terlebih dahulu bila akan melakukan analisis regresi berganda. Asumsi tersebut antara lain sebagai berikut:

1. Asumsi Normalitas
Asumsi Normalitas digunakan untuk mengetahui apakah data terdistribusi secara merata atau tidak. Uji ini untuk meyakinkan apakah data bersifat parametrik (terukur) atau nonparametrik (tidak terukur) karena kedua jenis data tersebut menggunakan alat analisis yang berbeda. Ketikda data dikatakan Normal maka dilakukan analisis Parametrik seperti Regresi. Sedangkan untuk data yang tidak Normal (Nonparametrik) maka alat analisisnya adalah Uji Komparasi.

2. Asumsi Multikolinierita
Asumsi Multikolinieritas digunakan untuk mengetahui apakah terdapat hubungan antar masing-masing variabel bebas atau independent yakni X1, X2, X3 dan seterusnya. Ketika terdapat hubungan antara X1 dan X2 maka analisis regresi berganda tidak dapat dilakukan karena variabel tersebut bisa dijadikan satu dan akan kembali menjadi analisis regresi sederhana.

3. Asumsi Heterokedastisitas
Asumsi Heterokedastisitas digunakan untuk mengetahui banyaknya data residu atau yang tidak terukur atau data yang kesalahannya semakin tinggi disebabkan meningkatnya jumlah variabel. Jika awalnya regresi sederhana hanya pengaruh X ---> Y maka tingkat kesalahannya akan semakin meningkat jika terdapat variabel X1, X2, X3, X4 dan X5 terhadap Y. Oleh karena itu perlu diluruskan kembali seberapa jauh banyaknya nilai residu tersebut ketika ditambahkan banyak variabel.

4. Asumsi Autokorelasi.
Autokorelasi dilakukan untuk jenis data Time Series yakni data yang terdiri dari tahun ke tahun. Antara tahun satu dengan berikutnya tidak boleh berhubungan satu sama lain. Dalam latihan ini sebenarnya tidak diperlukan Autokorelasi karena data berbentuk Cross-Section namun tetap dijelaskan sebagai pembelajaran pada jenis data Time Series nantinya.

Asumsi tersebut akan kita bahas dalam Uji Asumsi Klasik. Ketika suatu persamaan Regresi mengalami masalah dengan Asumsi Klasik data tersebut harus dibenahi terlebih dahulu. Berikut ini langkah-langkah dalam melakukan uji asumsi klasik:

1. Lakukan Input data seperti di bawah ini:

Input data diatas merupakan nilai rata-rata dari setiap indikator atau item pertanyaan, kita juga bisa menggunakan nilai total skor.

2. Langkah selanjutnya adalah klik Analyze --> Regression --> Linier maka akan muncul kotak dialog seperti di bawah ini:

Masukan variabel X1,X2,X3,X4 dan X5 dalam kolom Independet (Variabel Bebas) lalu masukkan Variabel Y dalam kolom Dependent (Variabel Terikat).

3. Langkah selanjutnya klik tombol Statistics lalu akan muncul kotak dialog seperti gambar di bawah ini:

Lalu centang Colinierity Diagnostics dan Durbin Watson untuk mengetahui hasil Multikolonieritas dan Autokorelasi. Lalu kilik Continue.

4. Langkah selanjutnya klik menu Plot maka akan muncul kotak dialog seperti gambar di bawah ini:

Masukkan ZPRED pada kolom X dan SRESID pada kolom Y lalu centang Histogram dan Normal Probability Plot untuk melihat Normalitas data dan Hetereokrdastisitas lalu klik Continue

5. Selanjutnya klik OK dan hasilnya akan muncul seperit di bawah ini:

Hasil analisis diatas menandakan bahwa nilai Durbin Watason adalah 1,544. Data terbebebas dari Autokorelasi jika berada diantara nilai -2 dan 2 sehingga persamaan regresi diatas terbebebas dari Autokorelasi.

Selanjutnya untuk melihat Mulitikolinieritas ditinjau dari nilai Tollerance dan VIF. Nilai Tollerance yang dibutuhkan adalah harus lebih besar dari 0,1. Nilai VIF yang dibutuhkan harus kurang dari 3. Berdasarkan hasil diatas dapat disimpulkan tidak terjadi Multiokolinieritas dalam persamaan regresi.

Hasil analisis diatas menunjukkan Normalitas suatu data. Pertama perhatikan grafik Histogramnya. Data dikatakan normal bila kurva berbentuk Lonceng. Dilihat dari gambar diatas sudah berbentuk lonceng maka data dapat dikatakan Normal. Kedua dilihat dari Plot. Data dikatakan normal bila titik-titik plot searah dengan garis dan saling terikat satu sama lain. Melihat gambar plot diatas dapat dikatakan bahwa data berdistribusi Normal.

Adakalanya Uji diatas kurang meyakinkan karena tidak memberikan angka yang pasti dan hanya berupa Gambar saja. Agar lebih meyakinkan dengan angka maka Akan kita lakukan Uji Kolmogrov Smirnof di pembahasan berikutnya.

Hasil analisis diatas menunjukkan ada atau tidaknya Heterokedadstisitas dalam data. Data dikatakan tidak ada heterokedastisitas bila titik-titik plot menyebar secara merata dan tidak membentuk pola tertentu. Meninjau gambar diatas diketahui bahwa titik-titik plot tidak menyebar secara merata bahkan cenderung membentuk pola bergaris-garis sehingga ditengarai terdapat Heterokedastisitas dalam data.

Sekali lagi bahwa hanya dengan gambar akan terlihat kurang meyakinkan. Oleh karena itu agar memperoleh angka statistik yang meyakinkan kita lakukan Uji Glejser yang akan dibahas bersamaan dengan Uji Klmogrov nanti.

UJI KOLMOGROV SMIRNOF (Normalitas) dan UJI GLEJSER (Heterokedastisitas)

Langkah pertama dalam melakukan kedua analisis tersebut hampir sama yakni klik Analyze --> Regression --> Linear maka akan muncul kotak dialog seperti di bawah ini

Pertama reset ulang kembali data agar tidak menumpuk pada hasil analisis nanti, lalu masukkan variabel X1,X2,X3,X4,dan X5 pada kolom Independent dan Y pada Dependent. Lalu klik tombol Save maka akan muncul kotak dialog seperti dibawah ini

Centang pada kolom Residual --> Unstandardized ----> Klik Continue lalu Ok

Angka yang kita butuhkan akan muncul pada menu Input Data bukan pada Output yakni pada Baris RES_1 seperti dibawah ini

Melalui angka tersebut kita akan mengetahui Normalitas suatu data dengan Uji Kolmogrov Smirnov yakni dengan cara klik menu Analyzed ---> Nonparametric Test ---> Legacy Dialog ---> 1 sample K seperti dibawah ini

Hasilnya akan muncul kotak dialog seperti dibawah ini

Masukkan Variabel Unstandardized Residual yang sudah kita peroleh tadi lalu centang kolom Normal dan klik OK maka akan menghasilkan output seperti di bawah ini:

Berdasarkan hasil diatas Data dapat dikatakan normal jika nilai signifikansi berada diatas 0,05 maka data diatas dikatakan Normal karena nilai signifikanis 0,200>0,05.

Selanjutnya untuk melakukan Uji Glejser dalam mengetahu Heterokedastisitas dapat dilakukan dengan cara yang sama bedanya kita abosolutkan nilai residual atau RES_1 yang sudah kita peroleh tadi.

Caranya kita klik Transform ---> Compute Variable maka akan muncul kotak dialog seperti gambar di bawah ini

Maka akan muncul Kotak dialog seperti dibawah ini:

Klik Function Group All ---> pilih Abs ---> naikkan ke atas,

Lalu masukkan Unstandardized Residual pada kolom di kiri keatas juga lalu beri nama Target Variabel AbsoultResidual (tanpa spasi) klik OK seperti pada gambar dibawah ini

Maka akan menghasilkan angka seperti dibawah ini

Setelah mendapatkan nilai Absolut Residual maka Regresikan kembali variabel X1 sampai X5 dengan Absolut Residual tadi dengan cara klik Analiyzed ----> Regression ---> Linear maka akan muncul kotak dialog seperti di bawah ini

Masukkan variabel X1 sampai X5 pada dependent lalu untuk Independent masukkan Absoult Residual tadi lalu klik Ok Hasilnya seperti di bawah ini:

Lihat pada tabel Coefficent kolom Sig. diketahui bahwa masing-masing variabel akan terjadi heterokedastisitas bila memiliki pengaruh dengan variabel residu (yang tidak terukur). Semakin berpengaruh maka residunya akan membuat persamaan menjadi kurang bagus. Dikatakan berpengaruh bila memiliki nilai dibawah 0,05. Berdasarkan kolom tadi dapat dikatakn hanya variabel X4 yang memiliki nilai dibawah 0,05 yakni 0,03< 0,05. Maka Variabel X4 mengalami masalah heterokedastisitas dan harus dikeluarkan dalam persamaan.

Demikian langkah-langkah dalam melakukan Uji Asumsi Klasik Semoga Bermanfaat.

Soal Tutorial Statistik

Untuk soal ujian turial aplikom statistik bisa diunduh data excel di sini SOAL UJIAN TUTORIAL APLIKOM STATISTIK

Cara Uji Instrumen (Validitas dan Reliabilitas)

Dalam melakukan penelitian kuantitatif umumnya menggunakan instrumen penelitian berupa kuesioner yang terdiri dari beberapa item pertanyaan dengan variasi jawaban mulai dari 1 (sangat tidak setuju) hingga 5 (sangat setuju) yang dikenal dengan Skala Likert.

Sebuah kuesioner dapat dikatakan Valid apabila dapat mengukur apa yang ingin diukur (ibarat penggaris dapat mengukur panjang suatu benda) dalam hal ini adalah persepsi responden yang sesungguhnya. Selain itu Kuesioner harus reliabel yakni memiliki pengukuran yang konsisten baik digunakan dari waktu ke waktu maupun objek penelitian yang berbeda.

1. UJI VALIDITAS

Pertama buka data SPSS seperti pada tutorial sebelumnya di tautan ini Input Data SPSS

Selanjutnya pilih menu Analize --> Correlate --> Bivariat seperti gambar berikut

Selanjutnya akan muncul kotak dialog seperti berikut

Masukkan item pertanyaan X1.1 sampai TotX1 ke kotak Variabel lalu klik Ok.

Hasilnya adalah sebagai berikut

Berdasarkan hasil diatas diketahui bahwa nilai korelasi antara Item beserta nilai Skor berada diatas 0,3 serta nilai signifikansi berada dibawah 0,05 yang menunjukkan adanya korelasi atau hubungan yang kuat masing-masing item pertanyaan dengan jumlah seluruh item pertanyaan. Berdasarkan asumsi tersebut Kuesioner dapat dikatakan Valid. Pendapat ini dikutip dalam buku Sugiono Metodologi Penelitian Bisnis.

Adakalanya uji validitas perlu melihat nilai korelasi atau hubungan antar masing-masing Item yang umumnya disebut dengan Validitas Kovergen yakni melihat hubungan antar item-item yang membangun sebuah konstruk yang dijelaskan secara teoritis.

Langkah-langkah dalam melakukan uji Validitas untuk item pertanyaan X2 hingga Y dapat dilakukan mengulangi langkah diatas.

2. UJI RELIABILTAS

Pertama buka menu Analyze --> Scale --> Reliability Analysis seperti gambar dibawah ini

Maka akan muncul kotak dialog seperti di bawah ini

Masukkan item X1 hingga X4 ke kotak Item lalu isi label sesuai dengan nama Indikator yang diuji dalam data ini Indikator bernama Bukti Fisik lalu klik Ok hasilnya dapat dilihat seperti berikut

Berdasarkan hasil uji reliablitas diketahui nilai Cronbach's Alpha untuk 4 Item pertanyaan
Nilai Cronbach's Alpha minimal harus lebih dari 0,7 namun diatas 0,6 masih diperbolehkan.
Untuk Variabel selanjutnya yakni X2 hingga Y bisa diulangi dengan proses yang sama.

Demikian langkah-langkah dalam Uji Validitas dan Reliabilitas semoga bermanfaat.

Cara melakukan Analisis Deskriptif

Analisis Deskriptif diperlukan dalam mengetahui bagaimana tanggapan responden secara rata-rata serta mengetahui jumlah responden yang menjawab sangat tidak setuju yang dinotasikan dengan angka 1 dan sangat setuju dinotasikan dengan angka 5 pada skala Likert. Langkah-langkah melakukan analisis statistik deskriptif antara lain sebagai berikut:

Pertama input input data ke SPSS seperti yang dijelaskan sebelumnya dalam tautan ini INPUT DATA SPSS

Setelah itu buka menu Analyze --> Descriptive Statistics --> Frequencies seperti berikut

Lalu akan muncul kotak dialog seperti dibawah ini dan pindahkan Item X1.1 sampai X1.4 ke kolom Variabel lalu klik Statistics

Selanjutnya akan muncul kotak dialog seperti berikut lalu centang Mean (sesuai dengan kebutuhan, dalam tutorial ini hanya dibutuhkan nilai rata-rata) lalu klik Continue

Maka akan muncul hasil pada jendela yang lain seperti pada gambar di bawah ini

Hasil analisis menunjukkan bahwa untuk Item Pertanyaan 1 dari 100 responden (Data dari 100 Sampel) memiliki nilai rata-rata 3,92 yang menunjukkan bahwa rata-rata Setuju (mendekati 4) dengan pertanyaan yang diajukan.

Tabel yang dibawahnya menunjukkan bahwa untuk jawaban 5 (tidak setuju) hanya satu responden yang menjawab sedangkan untuk 4 (sangat setuju) 63 responden.

Untuk Item pertanyaan Variabel X2 hingga Y dapat diulangi proses seperti sebelumnya. Semoga Bermanfaat.

Cara Input Data SPSS

SPSS merupakan software statistik yang bersifat umum digunakan dalam penelitian khusunya skripsi, thesis maupun disertasi. Penggunaan SPSS memudahkan dalam melakukan analisis data karena akan sangat sulit dan membutuhkan waktu lama bila melakukan dengan hitungan secara manual. Berikut ini akan dijelaskan langkah-langkah dalam melakukan input data ke SPSS.

Pertama tabulasikan kuesioner anda ke dalam Ms Excel seperti data berikut (Unduh Data) DATA EXCEL